Question

1. One number is 6 more than another number the sum of twice the smaller number and three timesthe larger number is −7 (let `x’ be the number). Construct an equation in terms of x, and use it to find the number `x’.

Answer 1

Given the question, the following are the solution steps to answer the question.

STEP 1: Represent the unknown numbers with variable x and y

`\begin{gathered} \text{From statement 1} \\ x=y+6----\text{equation 1} \\ \text{This implies that x is the bigger number and y is the smaller number} \\ \text{From statement 2} \\ \text{ sum of twice the smaller num}ber=2y \\ \text{thr}ee\text{ times the larger number}=3x \\ \text{Result is -7, then,} \\ 3x+2y=-7-----\text{equation 2} \end{gathered}`

STEP 2: Write out the derived equations

`\begin{gathered} x=y+6---\text{equation 1} \\ 3x+2y=-7---\text{equation 2} \\ \text{making x the subject of equation 2} \\ 3x=-7-2y \\ \text{Divide both sides by 3} \\ (3x)/(3)=(-7-2y)/(3) \\ x=(-7-2y)/(3) \end{gathered}`

STEP 3: Solve for x

`\begin{gathered} x=y+6 \\ x-6=y \\ \text{substitute x-6 for y in equation 2} \\ 3x+2(x-6)=-7 \\ 3x+2x-12=-7 \\ 5x-12=-7 \\ \text{Add 12 to both sides} \\ 5x-12+12=-7+12 \\ 5x=5 \\ \text{Divide both sides} \\ (5x)/(5)=(5)/(5) \\ x=1 \end{gathered}`

Hence, the equation in terms of x is:

`\begin{gathered} x=y+6 \\ x=(-7-2y)/(3) \end{gathered}`

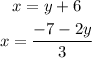
And the value of x is 1