SOLUTION
Given the question, the following are the solution steps to answer the question.
STEP 1: Represent the unknown numbers with variable x and y

STEP 2: Write out the derived equations
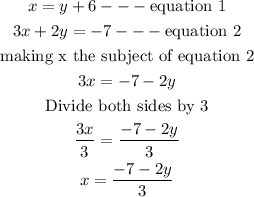
STEP 3: Solve for x

Hence, the equation in terms of x is:
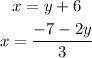
And the value of x is 1