Question

Match each inequality with the correct solution.

Answer 1

i. = b

ii = d

iii = a

iv = c

Explanation:

When dividing an inequality with a negative number, remember to flip the inequality symbol:

• Less than (<) flips to greater than(>).
• Less than or equal to (≤) flips to greater than or equal to (≥).

..................................................................................................................................................

`\sf I.\ \boldsymbol{\sf 4x + 12 < 20}`

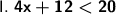
`\sf \implies 4x + 12 - 12 < 20 - 12\ \textsf{[ Subtract \boldsymbol{\sf 12} from both sides. ]}`

`\sf \implies 4x < 8\ \textsf{[ Divide both sides by \boldsymbol{\sf 4}. ]}`

`\sf \implies (4x)/(4) < (8)/(4)\ \textsf{[ Simplify. ]}`

`\sf \implies \boxed{\sf x < 2}`

..................................................................................................................................................

`\sf II.\ \boldsymbol{\sf 55 < 35 + 10x}`

`\sf \implies 55 - 35 < 35 - 35 + 10x\ \textsf{[ Subtract \boldsymbol{\sf 35} from both sides. ]}`

`\sf \implies 20 < 10x\ \textsf{[ Divide both sides by \boldsymbol{\sf 10}. ]}`

`\sf \implies (20)/(10) < (10x)/(10)\ \textsf{[ Simplify. ]}`

`\sf \implies 2 < x \implies \boxed{\sf x > 2}`

..................................................................................................................................................

`\sf III.\ \boldsymbol{\sf -(3)/(2)x + 12 > 15}`

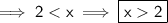
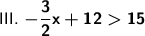
`\sf \implies -(3)/(2)x + 12 - 12 > 15 - 12\ \textsf{[ Subtract \boldsymbol{\sf 12} from both sides. ]}`

`\sf \implies -(3)/(2)x > 3\ \textsf{[ Multiply both sides by \boldsymbol{\sf 2}. ]}`

`\sf \implies 2\left(-(3)/(2)x\right) > 2(3)`

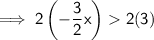
`\sf \implies -3x > 6\ \textsf{[ Divide both sides by \boldsymbol{\sf -3}. ]}`

`\sf \implies (-3x)/(-3) > (6)/(-3)\ \textsf{[ Simplify. ]}`

`\sf \implies \boxed{\sf x < -2}`

..................................................................................................................................................

`\sf IV.\ \boldsymbol{\sf -8x < 16}`

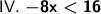
`\sf \implies (-8x)/(-8) < (16)/(-8)\ \textsf{[ Divide both sides by \boldsymbol{\sf -8}. ]}`

`\sf \implies \boxed{\sf x > -2}`

..................................................................................................................................................