ANSWERS
Part A: student B's answer is incorrect. They made a mistake in step 3. See the explanation for the details about the mistakes
Part B: see the explanation
Step-by-step explanation
PART A
Let's simplify the expression first. This way we will see what should the final answer be and then we can compare it with the students' answers.
First, we can distribute the denominator into the subtraction,

Then we have to replace the cosecant with its equivalent, since it is the reciprocal of the sine,
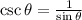
Replacing we have,
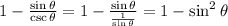
From the following trigonometric identity,

We know that,
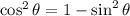
Hence, the simplified expression is cos²θ.
Therefore, we can conclude that student B simplified the expression incorrectly. Steps 1 and 2 are correct. Although they are not the same used here, those steps are correctly solved. Then, in step 3 the student replaced 1 - sin²θ as we did, but a mistake was made in the denominator because, instead of canceling out the sine, the student wrote sin²θ. This probably happened because the student replaced the cosecant by the sine of the angle instead of its reciprocal.
PART B
As stated in part A, student B made a mistake in step 3, where they replaced the cosecant with the sine,
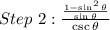
For step 3, the following formula must be used,
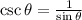
So, step 3 is,
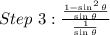
Then, in the next step, we simplify this division,
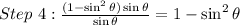
And then, we simplify using the trigonometric identity named in part A,
