Question

Consider the function ƒ(x) = (x + 1)2 – 1. Which of the following functions stretches ƒ(x) vertically by a factor of 4?Question 1 options:A) ƒ(x) = (1∕4x + 1)2 + 3B) ƒ(x) = 1∕4(x + 1)2 – 4C) ƒ(x) = 4(x + 1)2 – 1D) ƒ(x) = 4(4x + 1)2 – 1

Answer 1

A vertical stretch occurs when a base graph is multiplied by a certain factor (say a), that is greater than 1. This results in the graph being pulled outward but retaining the input values (or x).

When a function is vertically stretched, we expect its graph’s y values to be farther from the x-axis.

When we have |a| > 1, a · f(x) will stretch the base function by a scale factor of a. The input values will remain the same, so the graph’s coordinate points will now be (x, ay). This means that if the base graph is of the function f(x) with a factor of a, then the resulting graph function will be a x f(x),

`\begin{gathered} \text{The base graph function f(x)} \\ \text{ }f(x)\text{ vertically stretched by a factor of a will give a resulting graph function of} \\ a* f(x) \end{gathered}`

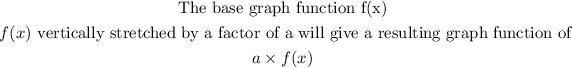
Given a base function f(x) as shown below

`f(x)=(x+1)^2-1`

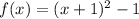
If stretched by a factor of 4. The resulting graph function would be as shown written below

`\begin{gathered} \text{resulting graph function is} \\ f(x)=4*((x+1)^2-1) \end{gathered}`
`f(x)=4(x+1)^2-4`
`f(x)=4((x+1)^2-1)`

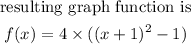
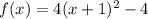
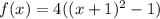
Hence, the resulting function is f(x)= 4 ((x+1)²-1)