Question

The ramp of a moving truck touches the ground 16 feet away from the end of the truck. If the ramp makes an angle of 14 relative to the ground, what is the length ofthe ramp?

Answer 1

Let's draw an illustration.

Assuming that the end of the truck is right angled to the ground, we can solve for the length of the ramp using cosine function.

`\cos \theta=\frac{adjacent\text{ side of the angle}}{\text{hypotenuse}}`

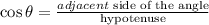
Based on the diagram, the angle is 14° and the length of the side adjacent to the angle is 16ft. However, the length of the ramp or the hyptenuse is missing. We are going to solve for the hypotenuse.

Let's plug in the given information to the cosine function.

`\cos 14=\frac{16ft}{\text{hypotenuse}}`

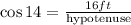
Cross multiply the function. Assume hypotenuse = x.

`x\cos 14=16ft`

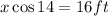
Divide both sides of the equation by cos 14.

`\begin{gathered} (x\cos14)/(\cos14)=(16ft)/(\cos14) \\ x=16.49ft \end{gathered}`

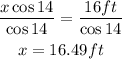
Therefore, the length of the ramp is approximately 16.49 ft.