Question

Solve by factoring (find the x-intercepts)x + 3x2 - 18x = 0x = 0, x= 3, x= -18x = 0, x=9, r = 2x=0, x= 3, x = -6x = 0, x= -3, x = 6

Answer 1

Solving equations by factoring

We are required to solve the equation:

`x^3+3x^2-18x=0`

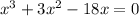
We need to find the expressions that factor the equation and then solve each factor separately.

First, note all terms have at least one x. There is no independent term. Thus, we can factor out x, as follows

`x(x^2+3x-18)=0`

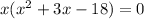
Now we have to find two numbers whose product is -18 and sum is +3

Those numbers are +6 and -3. Please note

+6 - 3 = +3

6*(-3) = -18

Now we factor as follows:

`x(x+6)(x-3)=0`

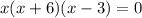
Since the result of a product is zero, any of them can be equated to zero, thus the solutions of the equations come from:

x = 0

x + 6 = 0

x - 3 = 0

The first solution comes directly (x=0)

The second solution is

x = -6

And the third is

x = 3