From the information given in the statement, you can see that the original function, before the transformation, is
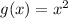
Now, by the rules of transformation of functions you know that:
*g(x - h) moves the function g(x) h units right
*g(x) + k moves the function g(x) k units up
So, in this case, you have
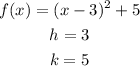
Which implies that the original graph will move 3 units to the right and 5 units up.
Therefore, the graph that represents the given quadratic function is the graph of option B.