Given data:
* The angle of incidence in the medium A is,
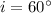
* The angle of refraction in medium B is,
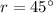
Solution:
According to the Snell's Law,
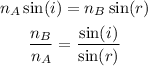
where n_B is the refractive index of medium B and n_A is the refractive index of medium B,
Substituting the known values,
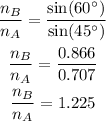
Thus, the ratio of refractive index of medium B to the refractive index of medium A is 1.225.