Question

What is the height of a right triangle with an angle that measures 60 degrees and a base of 12. The 60 degree angle is opposite to the base.

Answer 1

To solve this problem we can use some trigonometric relations. In a right triangle, given an angle, the ratio between the opposite leg to this angle, and the adjacent leg to this angle is equal to its tangent.

Our angle is 60 degrees, the opposite side measures 12, and the adjacent side is the height is what we want to know(let's call it h). Then, we have

`\tan (60^o)=(12)/(h)`

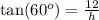
The tangent of 60º is a known value. It is the square root of 3, then, we have

`\sqrt[]{3}=(12)/(h)`

Solving for h:

`\begin{gathered} \sqrt[]{3}=(12)/(h) \\ \sqrt[]{3}h=12 \\ h=\frac{12}{\sqrt[]{3}} \\ h=4\sqrt[]{3} \end{gathered}`

The height of this triangle is 4 times the square root of 3.