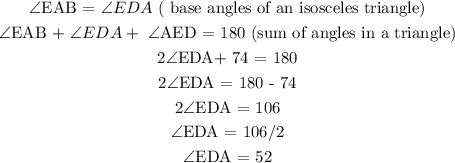AE = 15
∠EDA = 52°
Step-by-step explanation:
The sahpe has been given as a rectangle.
In a rectangle, the diagonals bisect each other and they are equal to each other.
The given diagonals:
BD = 4x - 2
AC = 5x - 10
We find the value of x by equating the diagonals:
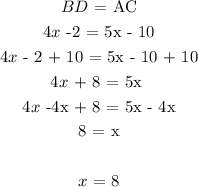
Since the diagonals bisect each other,
AE = EC
DE = EB
To find AE:
AE + EC = AC
AE + AE = AC
AC = 5x - 10 = 5(8) - 10 = 30
2AE = 30
AE = 30/2
AE = 15
To get ∠EDA:
∠EAB = 37°