When dealing with a trinomial of the form:
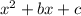
Compare the expression to that of a perfect square trinomial:
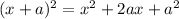
We want 2a=b, so we can add a^2 - a^2 to be able to write the trinomial as a squared binomial plus a constant. Since a=b/2, we should add b^2/4 - b^2/4.
C)
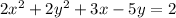
First, notice that the coefficient of x^2 and y^2 is not 1. We need it to be equal to 1 in order to use the former procedure. Divide both sides by 2:
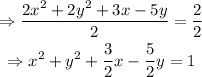
The coefficient of x is 3/2, and comparing to the formula of the perfect square trinomial, then:
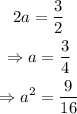
Te coefficient of y is -5/2, and comparing to the formula of the perfect square trinomial, the constant term inside the binomial should be -5/4, so we need a constant term of 25/15 to complete the square. Add 9/16 and 25/16 to both sides of the equation:
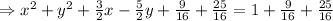
Reorder the terms on the left hand side of the equation, and simplify the expression on the right hand side:
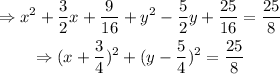
The coordinates of the center of this circle, are:
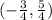
The radius is given by the square root of the constant term on the right hand side of the equation:
![\begin{gathered} r=\frac{\sqrt[]{25}}{8} \\ \Rightarrow r=(5)/(4)\sqrt[]{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/matz54b146hzjr3dv6ihdt6a45nfdpltlm.png)
D)
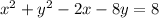
The coefficient of x is -2, which should be twice the constant term inside the squared binomial. So, that constant term is -1, and (-1)^2=1. Add 1 to both sides and rewrite the polynomial on x as a squared binomial:
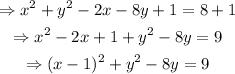
The coefficient of y is -8, which should be twice the constant term inside the squared binomial. So, the constant term is -4, and (-4)^2=16. Add 16 to both sides and rewrite the polynomial on y as a squared binomial:
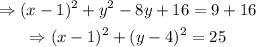
The coordinates of the center of this circumference are (1,4), and the radius is equal to 5.