Question

1. Complete the squares for each quadratic, list the center and radius, then graph each circle.C) and D)

Answer 1

When dealing with a trinomial of the form:

`x^2+bx+c`

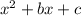
Compare the expression to that of a perfect square trinomial:

`(x+a)^2=x^2+2ax+a^2`

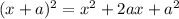
We want 2a=b, so we can add a^2 - a^2 to be able to write the trinomial as a squared binomial plus a constant. Since a=b/2, we should add b^2/4 - b^2/4.

C)

`2x^2+2y^2+3x-5y=2`

First, notice that the coefficient of x^2 and y^2 is not 1. We need it to be equal to 1 in order to use the former procedure. Divide both sides by 2:

`\begin{gathered} \Rightarrow(2x^2+2y^2+3x-5y)/(2)=(2)/(2) \\ \Rightarrow x^2+y^2+(3)/(2)x-(5)/(2)y=1 \end{gathered}`

The coefficient of x is 3/2, and comparing to the formula of the perfect square trinomial, then:

`\begin{gathered} 2a=(3)/(2) \\ \Rightarrow a=(3)/(4) \\ \Rightarrow a^2=(9)/(16) \end{gathered}`

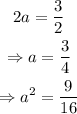
Te coefficient of y is -5/2, and comparing to the formula of the perfect square trinomial, the constant term inside the binomial should be -5/4, so we need a constant term of 25/15 to complete the square. Add 9/16 and 25/16 to both sides of the equation:

`\Rightarrow x^2+y^2+(3)/(2)x-(5)/(2)y+(9)/(16)+(25)/(16)=1+(9)/(16)+(25)/(16)`

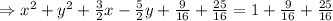
Reorder the terms on the left hand side of the equation, and simplify the expression on the right hand side:

`\begin{gathered} \Rightarrow x^2+(3)/(2)x+(9)/(16)+y^2-(5)/(2)y+(25)/(16)=(25)/(8) \\ \Rightarrow(x+(3)/(4))^2+(y-(5)/(4))^2=(25)/(8) \end{gathered}`

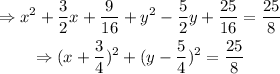
The coordinates of the center of this circle, are:

`(-(3)/(4),(5)/(4))`

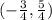
The radius is given by the square root of the constant term on the right hand side of the equation:

`\begin{gathered} r=\frac{\sqrt[]{25}}{8} \\ \Rightarrow r=(5)/(4)\sqrt[]{2} \end{gathered}`

D)

`x^2+y^2-2x-8y=8`

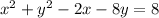
The coefficient of x is -2, which should be twice the constant term inside the squared binomial. So, that constant term is -1, and (-1)^2=1. Add 1 to both sides and rewrite the polynomial on x as a squared binomial:

`\begin{gathered} \Rightarrow x^2+y^2-2x-8y+1=8+1 \\ \Rightarrow x^2-2x+1+y^2-8y=9 \\ \Rightarrow(x-1)^2+y^2-8y=9 \end{gathered}`

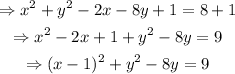
The coefficient of y is -8, which should be twice the constant term inside the squared binomial. So, the constant term is -4, and (-4)^2=16. Add 16 to both sides and rewrite the polynomial on y as a squared binomial:

`\begin{gathered} \Rightarrow(x-1)^2+y^2-8y+16=9+16 \\ \Rightarrow(x-1)^2+(y-4)^2=25 \end{gathered}`

The coordinates of the center of this circumference are (1,4), and the radius is equal to 5.