Answer
x = 4
Step-by-step explanation
Given:
The given quadratic equation is
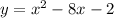
What to find:
To find the x-value of the vertex of the quadratic equation.
Step-by-step solution:
The solution involves two steps.
Step 1: Find the value of y at maximum (y-max)
The formula to get y-max is given by
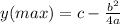
From the quadratic equation given, a = 1, b = -8 and c = -2
Therefore
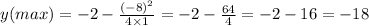
y-max = -18
Step 2: Determine x-vale at y-max.
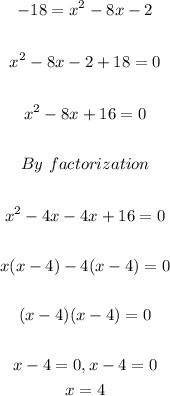
The x-value of the vertex is 4