To create the line, first, recall the definition of parallel lines.
Two lines are parallel if they have the same slope.
First, calculate the slope of line AB with A(-6,-1) and B(6,-9).
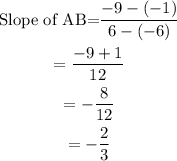
Point C is at (3,2).
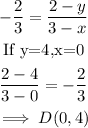
Draw a line to D(0,4) to create a parallel line.
If the line was extended, to determine if it passes through (18,-8), pick points C and (18,-8) and check if its slope is -2/3.
C(3,2) and (18,-8).
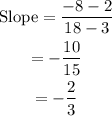
Since the slope is -2/3, it passes through the point (18,-8).