We have to express the probabilities as unreduced fractions.
The probability of choosing a person who has a Ford and has no complaints.
We can calculate the probability as the qoutient between the successful events and the total events.
The successful events are the persons that have a Ford and has no complaints. This number is 60.
The total number of persons we can choose from is 500.
Then, the probability is 60/500.
It can be reduced as:
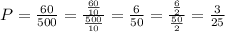
The probability of choosing a person who has a Ford or has No complaints.
In this case the number of successful events is the sum of the people that has a Ford (95 persons) and the people that has no complaints (178 persons).
Then, the probability is:
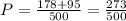
The probability of choosing a person who does not have a Ford.
The successful events in this case is the total (500) minus the people that have a Ford (95).
Then, the probability is:

Answer:
a) P = 3/25
b) P = 273/500
c) P = 81/500