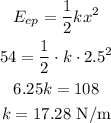a)
Since the force of 25 N is applied by a distance of 10 meters, we can calculate the work done:
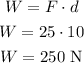
Then, if all the energy is kinetic energy, we can calculate the box speed:
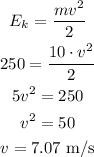
b)
The box slides up the hill, so part of the energy is now potential energy:
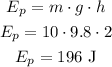
The remaining kinetic energy (250 - 196 = 54 J) will be converted into elastic potential energy of the spring: