Question

So I have a Kinematics question that I’m confused on.It says:A cargo helicopter, descending steadily at a speed of 4.0 m/s, releases a small package. Let upward be the positive direction for this problem.(a) If the package is 31 m above the ground when it is dropped, how long does it take for the package to reach the ground?(b) What is its velocity just before it lands?

Answer 1

a) t = 2.14 s

b) = -24.972 m/s

Step-by-step explanation:

We know that the initial height of the package is 31 m, and the final height is 0 m, additionally, its initial velocity is the velocity of the helicopter, so it is -4m/s because it is descending. Finally, the acceleration is due to gravity, so it is -9.8 m/s².

Now, we can use the following equation to find the time to reach the ground

`y_f=y_i+v_it+(1)/(2)at^2`

Where y is the height, v is the velocity, a is the acceleration and t is the time. Replacing the values, we get:

`\begin{gathered} 0=31-4t+(1)/(2)(-9.8)t^2 \\ 0=31-4t-4.9t^2 \end{gathered}`

So, we can find the roots for the quadratic equation as:

`\begin{gathered} t=\frac{-(-4)\pm\sqrt[]{(-4)^2-4(-4.9)(31)}}{2(-4.9)} \\ t=2.14\text{ and t = -2.96} \end{gathered}`

Since t = -2.96 has no sense in this case, the answer is t = 2.14. It means that the package takes 2.14 seconds to reach the ground.

On the other hand, we can calculate the final velocity using the following equation:

`v_f=v_i+at`

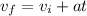
Replacing the values, we get:

`\begin{gathered} v_f=-4+(-9.8)(2.14) \\ v_f=-4-20.972 \\ v_f=-24.972\text{ m/s} \end{gathered}`

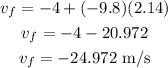
So, the velocity just before it lands is -24.972 m/s