The x-component of vector A is Ax = -5.50 m
The y-component of vector A is Ay = 7.50 m
We are asked to find the magnitude and the direction of the vector (counterclockwise from the +x-axis)
The magnitude of vector A is given by
![\begin{gathered} |A|=\sqrt[]{A_x+A_y} \\ |A|=\sqrt[]{(-5.50)^2+(7.50)^2_{}} \\ |A|=\sqrt[]{30.25+56.25} \\ |A|=\sqrt[]{86.50} \\ |A|=9.3\; m \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/e9cvjybeap7zssisn48fem1r9u8wvsyfp0.png)
So, the magnitude of vector A is 9.3 m
First, let us draw a diagram to better understand the problem.
The direction of vector A is given by
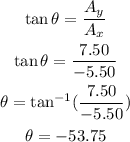
From the diagram, notice that θ lies in the second quadrant.
So, the counterclockwise direction from the positive x-axis is given by

So, the direction is 126.25° counterclockwise from the +x-axis.