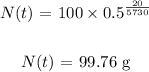Question

solve the following using logarithmic or exponential Carbon-14 is an element used to find the approximate age of a wide array of objects. It has a half life of 5,730 years. Find the amount of Carbon-14 on a 100g sample after 20 years.

Answer 1

`99.76\text{ g}`

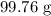
Step-by-step explanation:

Here, we want to calculate the amount of carbon-14 remaining

The formula to use here is as follows:

`N(t)=N_0((1)/(2))^{\frac{t}{t_{_{_(half)}}_{}}}`

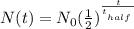
where:

N(t) is the mass left after some time or at a time t which is what we want to calculate

N_0 is the initial mass which is 100g in this case

t is the time which is 20 years

t_half is the half-life which is 5,730 years

Substituting these values, we have it that:

`\begin{gathered} N(t)\text{ = 100}*0.5^{(20)/(5730)} \\ \\ N(t)\text{ = 99.76 g} \end{gathered}`