Question

Hello, I am a little stuck on this question. May I get some help?

Answer 1

Equation:

`h^2+5h=155`

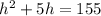
The Quadratic formula states that:

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

which in our case, x = h; and the variables a, b and c corresponds to the coefficients of an equation in the form:

`ax^2+bx+c=0`

Then, we have to rewrite our given equation in that form by subtracting 155 from both sides of the equation:

`h^2+5h-155=155-155`
`h^2+5h-155=0`

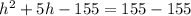
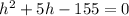
Now, based on this we can determine our variables:

• a = 1

,

• b = 5

,

• c = -155

Replacing these numbers in the Quadratic formula:

`h=\frac{-5\pm\sqrt[]{5^2-4\cdot(1)\cdot(-155)}}{2\cdot(1)}`

Simplifying:

`h=\frac{-5\pm\sqrt[]{25^{}+620}}{2}`
`h=\frac{-5\pm\sqrt[]{645}}{2}`

As the square root of 645 is not an exact root, to have an exact result we will leave this number like that until the result. Also, as we have a minus and plus sign before the root, this is the time where we divide the result into two variables (as there are two results):

`h_1=\frac{-5+\sqrt[]{645}}{2}\approx10.20`
`h_1=\frac{-5-\sqrt[]{645}}{2}\approx-15.20`

As the second result is negative, and we cannot have negative heights, then the height that will satisfy the desired area is 10.20 yards.

Answer: 10.20 yards