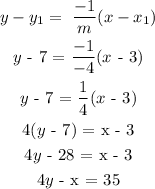Question

Using the points A(3,7) and B(2,11) find;A. The equation of the line parallel parallel to the line formed by the given points is what?

Answer 1

Answer:

4y - x = 35

Explanations:

The given points are A(3, 7) and B(2, 11)

The general equation of a line with the points A(x₁ , y₁) and B(x₂ , y₂) is :

`\begin{gathered} y-y_1=m(x-x_1) \\ \text{Where m is the slope } \\ m\text{ = }(y_2-y_1)/(x_2-x_1) \\ x_1=3,y_1=7,x_2=2,y_2=\text{ 11} \\ m\text{ = }(11-7)/(2-3) \\ m\text{ = -4} \end{gathered}`

Putting these values into the general line equation:

For the line parallel to the lines formed by the points slope = -1 / m

Slope = -1 / 4

`\begin{gathered} y-y_1=\text{ }(-1)/(m)(x-x_1) \\ y\text{ - 7 = }(-1)/(-4)(x\text{ - 3)} \\ y\text{ - 7 = }(1)/(4)(x\text{ - 3)} \\ 4(y\text{ - 7) = x - 3} \\ 4y\text{ - 28 = x - 3} \\ 4y\text{ - x = 35} \end{gathered}`