Question

A Ferris wheel at a carnival has a diameter of 54 feet. Suppose it turns at a rate of 10 revolutions per hour A) find the angular speed of the wheel in radians per hour B) Find the linear speed of passenger in feet per hour

Answer 1

Given data

*The given diameter of the Ferris wheel is d = 54 feet

*The given rate is 10 revolutions per hour

(A)

The angular speed of the wheel in radian per hour is calculated as

`\begin{gathered} \omega=2\pi*10 \\ =20*3.14 \\ =62.8\text{ radian/h} \end{gathered}`

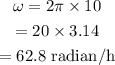
Hence, the angular speed of the wheel in radian per hour is 62.8 radian/h

(b)

The radius of the wheel is calculated as

`\begin{gathered} r=(d)/(2) \\ =(54)/(2) \\ =27\text{ } \end{gathered}`

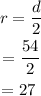
The formula for the linear speed of passengers in feet per hour is calculated as

`v=\omega r`

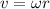
Substitute the values in the above expression as

`\begin{gathered} v=(62.8)(27) \\ =1695.6 \end{gathered}`

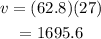
Hence, the linear speed of passengers in feet per hour is 1695.6 feet/hour