Given data
*The given diameter of the Ferris wheel is d = 54 feet
*The given rate is 10 revolutions per hour
(A)
The angular speed of the wheel in radian per hour is calculated as

Hence, the angular speed of the wheel in radian per hour is 62.8 radian/h
(b)
The radius of the wheel is calculated as
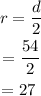
The formula for the linear speed of passengers in feet per hour is calculated as
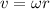
Substitute the values in the above expression as
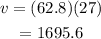
Hence, the linear speed of passengers in feet per hour is 1695.6 feet/hour