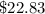Question

The monthly cost (in dollars) of a long-distance phone plan is a linear function of the total calling time (in minutes). The monthly cost for 43 minutes of calls is $18.21 and the monthly cost for 102 minutes is $24.70. What is the monthly cost for 85 minutes of calls?

Answer 1

The monthly cost for 85 minutes of call is;

`\text{\$22.83}`

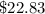
Step-by-step explanation:

Given that the monthly cost (in dollars) of a long-distance phone plan is a linear function of the total calling time (in minutes).

`C(x)=mx+b`

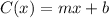
The monthly cost for 43 minutes of calls is $18.21 ;

`18.21=43m+b\text{ -------1}`

the monthly cost for 102 minutes is $24.70;

`24.70=102m+b\text{ -----------2}`

to get m and b, subtract equation 1 from 2;

`\begin{gathered} 24.70=102m+b \\ - \\ 18.21=43m+b \\ = \\ 6.49=59m \\ m=(6.49)/(59) \\ m=0.11 \end{gathered}`

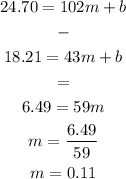
to get b, substitute the value of m into equation1;

`\begin{gathered} 18.21=43m+b \\ b=18.21-43(0.11) \\ b=18.21-4.73 \\ b=13.48 \end{gathered}`

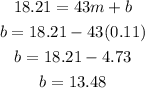
So, the linear function that can represent the monthly cost of phone plan is;

`C(x)=0.11x+13.48`

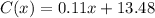
For the monthly cost for 85 minutes of call, we have;

`\begin{gathered} C(85)=0.11(85)+13.48 \\ C(85)=\text{ \$22.83} \end{gathered}`

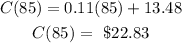
Therefore, the monthly cost for 85 minutes of call is;

`\text{\$22.83}`