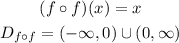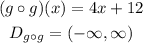Question

Consider the following functions.f(x) = 1/xg(x) = 2x + 4

Answer 1

Use the rule of correspondence of f and g as well as the definition of the composition of two functions to find the requested expressions.

Remember that given two functions, f₁ and f₂:

`(f_1\circ f_2)(x)=f_1(f_2(x))`

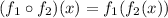
Since:

`\begin{gathered} f(x)=(1)/(x) \\ g(x)=2x+4 \end{gathered}`

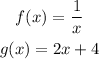
Then:

`\begin{gathered} (f\circ f)(x)=f(f(x)) \\ =(1)/(f(x)) \\ =(1)/(((1)/(x))) \\ =x \end{gathered}`

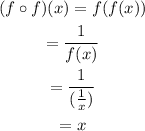
The domain of f(f(x)) must match the domain of f(x):

`D_(f\circ f)=D_f=(-\infty,0)\cup(0,\infty)`

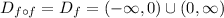
On the other hand:

`\begin{gathered} (g\circ g)(x)=g(g(x)) \\ =2\cdot g(x)+4 \\ =2(2x+4)+4 \\ =4x+8+4 \\ =4x+12 \end{gathered}`

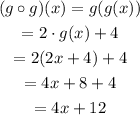
The domain is the same as the domain of g:

`(-\infty,\infty)`

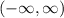
Therefore, the answers are:

`\begin{gathered} (f\circ f)(x)=x \\ D_(f\circ f)=(-\infty,0)\cup(0,\infty)_{} \end{gathered}`
`\begin{gathered} (g\circ g)(x)=4x+12 \\ D_(g\circ g)=(-\infty,\infty) \end{gathered}`