Consider that the equation of a straight line passing through two points is given by,
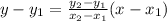
The points are given as,
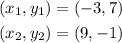
So the equation of line passing through these points is given by,
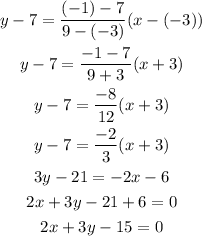
Thus, the equation of the line passing through the given points is 2x + 3y - 15 = 0 .