Question

A 0.900-kg block initially at rest on a frictionless, horizontal surface is acted upon by a force of 8.50 N for a distance of 4.00 m. How much farther would the force have to act for the block to have a speed of 11.8 m/s?answer in:____ m

Answer 1

0.51 m

Step-by-step explanation

Given:

• The mass of the block, m = 0.900 kg

,

• The block is initially at rest, so its initial velocity u = 0 m/s

,

• There is no friction

,

• The force applied horizontally, F = 8.50 N

,

• The distance the force is applied for, d = 4.00 m

Find:

• How much farther would the force have to act, x, for the block to have a speed of 11.8 m/s?

The work done by the force applied to the block, W, is equal to the change in its kinetic energy, KE,

`KE=W=F\cdot d=8.50N\cdot4.00m=34J`

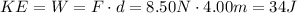
We know that the block was at rest, so the change in its kinetic energy is,

`KE=(1)/(2)m(v-u)^2=(1)/(2)mv^2`

We can find what is the speed of the block after the first 4 meters,

`v=\sqrt{(2KE)/(m)}=\sqrt{(2\cdot34J)/(0.9kg)}\approx8.69m/s`

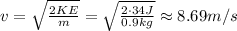
Now, we know that the force must act for a little farther so that the block has a speed of 11.8 m/s. In that distance, the block's kinetic energy changes as,

`KE_f=(1)/(2)m(v_f-v)^2=(1)/(2)\cdot0.9kg\cdot(11.8m/s-8.69m/s)^2\approx4.35J`

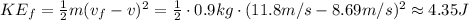
Following the same reasoning as before, this change in kinetic energy must be made by the work done, so, if the force applied is the same,

`W_f=KE_f=F\cdot x`

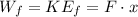
Solving for x,

`x=(W_f)/(F)=(KE_f)/(F)=(4.35J)/(8.50N)\approx0.51m`

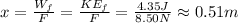
Hence, the force must be applied for another 0.51 m, rounded to two decimal places.