Question

The company sent you a Ferris wheel that has a radius of 40 ft. and each car is 5 ft. tall. The people can’t start to look for their houses until they get above the tents of the carnival and those tents are 20ft tall. The Ferris wheel has 20 passenger cars and it takes 12 minutes to have all the cars filled. Once all cars are filled the Ferris wheel runs at 1 rotation for every 2 minutes for a total of 8 minutes.a. Once someone has boarded the Ferris wheel, how long will it take for them to be able to start looking for their house?b. How long will they have to search for their house?

Answer 1

Step-by-step explanation

From the statement, we know that:

• the Ferris wheel has a radius R = 40 ft, and each car is h = 5 ft tall,

• the people can’t start to look for their houses until they get above the tents of the carnival and those tents are h = 20 ft tall,

,

• once all cars are filled the Ferris wheel runs at 1 rotation every 2 minutes for a total of 8 minutes.

Using the data of the problem, we make the following diagram:

When a car passes the heigh h = 20 ft, the passenger cars can start to look for their houses.

Height of the car as a function of time

We define the function y(t) which is the height of the car as a function of time. Because the cars move around a wheel, their vertical movement or height can be described by a sinusoidal function:

`y(t)=A\cdot\sin((2\pi t)/(T)+\phi)+B.`

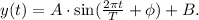
Where:

• A is the amplitude of the movement, which is A = R = 40 ft (the radius of the wheel),

,

• T is the period of a rotation, which is T = 2 min,

,

• B is the mean altitude (the altitude of the center of the wheel), which is B = 40 ft,

,

• φ is a phase that we must set to begin the movement from the ground at time t = 0.

Replacing these data in the general function above, we get:

`y(t)=40ft\cdot\sin(\frac{2\pi t}{2\text{ min}}+φ)+40ft.`

We set the phase φ such that we have an altitude y(0) = 0 ft for t = 0. We get that value when we have:

`y(0)=40ft\cdot\sin(\frac{2\pi\cdot0}{2\text{ min}}+φ)+40ft=40ft\cdot\sin(φ)+40ft=0.`

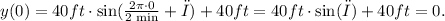
We satisfy this equation when we have:

`\sin(φ)=-1\Rightarrowφ=-(\pi)/(2).`

Replacing this value in the equation above, we have:

`y(t)=40ft\cdot\sin(\frac{\pi t}{\text{min}}-(\pi)/(2))+40ft.`

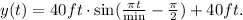
Plotting this function, we get the following graph:

a. Once someone has boarded the Ferris wheel, how long will it take for them to be able to start looking for their house?

We know that a person will be able to look once the altitude reaches 20 ft, so we must solve for t the equation:

`y(t)=40ft\cdot\sin(\frac{\pi t}{\text{1 min}}-(\pi)/(2))+40ft=20ft.`

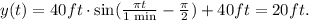
Solving for t, we get:

`\begin{gathered} 40ft\cdot\sin(\frac{\pi t}{1\text{ min}}-(\pi)/(2))=40ft-20ft, \\ \sin(\frac{\pi t}{1\text{ min}}-(\pi)/(2))=-(20ft)/(40ft), \\ \sin(\frac{\pi t}{1\text{ min}}-(\pi)/(2))=-(1)/(2), \\ \frac{\pi t}{1\text{ min}}-(\pi)/(2)=-(\pi)/(6), \\ \frac{\pi t}{1\text{ min}}=(\pi)/(2)-(\pi)/(6)=(\pi)/(3), \\ t=(1)/(3)\text{ min}=\frac{60\text{ s}}{3}=20\text{ s.} \end{gathered}`

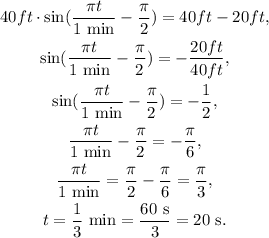
We have found that it will take 20 seconds for the passengers to be able to start looking for their house.

b. How long will they have to search for their house?

The passengers won't be able to see their houses once the car reaches again the 20 ft of altitude, that happens for the next value of t that satisfies the equation:

`\begin{gathered} \sin(\frac{\pi t}{1\text{ min}}-(\pi)/(2))=-(1)/(2), \\ \frac{\pi t}{1\text{ min}}-(\pi)/(2)=(7\pi)/(6), \\ \frac{\pi t}{1\text{ min}}=(\pi)/(2)+(7\pi)/(6)=(5\pi)/(3), \\ t=(5)/(3)\text{ min}=(5)/(3)\cdot60\text{ s}=100\text{ s.} \\ \\ \end{gathered}`

We see that between times t = 20 s and t = 100 s the passengers can look for their houses. So they have 100 s - 20 s = 80 s in each rotation to look for their houses. The wheel will round for 8 min, which means 8 min/2 min = 4 complete rotations. So the passengers will be able to look for their houses 4 * 80 s = 320 s in total.

Answer

a. Once the wheel starts to round, it will take 20 seconds for the passengers to start looking for their houses.

b. The passengers will have 80 seconds in each rotation to look for their houses and a total of 320 seconds in the trip.