We have 40 minutes to exercise, and we want to burn 300 calories.
The elliptical trainer burns 8 cal/min and the stationary bike burns 6 cal/min.
We can write the total amount of calories burned as:
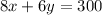
x: minutes in the elliptical trainer.
y: minutes in the stationery bike.
We also know that the total amount of minutes is 40, so we can write:
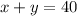
We can write y in function of x, and then solve the first equation:

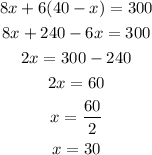
Then, for x=30, the value of y is:
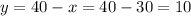
You should spend
30 minutes on the elliptical trainer and
10 minutes on the stationary bike.