Given:
f(x) = -10(x - 5) + 7
Use slope intercept form:
y = mx + b
Find the y-intercept for g(x) = x
The y-intercept, b = 0
Slope, m1 = 1
Find the y-intercept for, f(x) = -10(x - 5) + 7
f(x) = -10x + 50 + 7
f(x) = -10x + 57
y-intercept, b = 57
slope, m2 = -10
We have the following y-intercepts
b1 = 0
b2 = 57
The vertical shift is = b2 - b1 = 57 - 0 = 57
This means there was a transformation of 57 units upward.
Find the vertical stretch:
Since m2 is greater than m1, the graph is vertically stretched
Also, m1 and m2 have opposite signs, this means there was a reflection about the y-axis.
Therefore, the transformations are:
Translated 57 units upward
Vertical stretch
Reflection about the y-axis
The vertex is the point where the fuction changes direction.
This equation is not a parabola so it has no vertex
ANSWER:
Translated 57 units upward
Vertical stretch
Reflection about the y-axis
Also, If the correct function is:
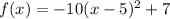
Use the function:
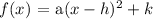
The parent function is:
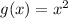
The transformations here are:
-5 indicates a horizontal shift of 5 units to the right
+7 indicates a vertical shift of 7 units upward
There was a reflection about the x-axis
The graph was vertically stretched
The vertex here is: (h, k) ==> (5, 7)