Question

Determine the maximum height of each tunnel. Is the truck able to pass through either tunnel without damage? If so, which tunnel(s) and why? Show your work. Note: This has to do with Pre-Calculus Conic Sections

Answer 1

First of all, let's make a plot of each curve:

Now, with these pictures in mind, let's compute the heigh of each one, which is measured from x = 0.

1) Circle

We see that the x-axis passes through the centre of the circle, so the height of the circular tunnel is equal to its radius. The general equation of a circle is:

`(x-x_0)^2+(y-y_0)^2=r^2.^{}`

Where (x0,y0) are the coordinates of the centre, and r is the radius.

Comparing the general equation with the equation of the problem, we see that:

`r^2=144\Rightarrow r=\sqrt[]{144}=12.`

So the heigh of the circular tunnel is H_c = 12.

2) Parabola

We see that the axis of symmetry of the parabola is parallel to the y-axis. The height of the tunnel with the parabola's form is the vertical distance between the x-axis and the vertex of the parabola. The general equation of a parabola is:

`y=a\cdot(x-h)^2+k.`

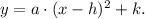
Where (h,k) are the coordinates of the vertex.

The equation of the parabola for this problem is:

`\begin{gathered} 4\cdot(-4)\cdot(y-16)=(x-18)^2, \\ -16\cdot(y-16)=(x-18)^2, \\ y-16=-(1)/(16)\cdot(x-18)^2, \\ y=-(1)/(16)\cdot(x-18)^2+16. \end{gathered}`

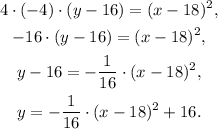
Comparing the general equation with the equation of the problem, we see that:

`(h,k)=(18,16)\text{.}`

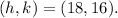
The vertical distance from the x-axis to the vertex is 16.

So the height of the tunnel with parabola's form is H_p = 16.

1) The maximum height of each tunnel is:

• 12 feet for the circular tunnel,

,

• 16 feet for the tunnel with parabola's form.

2) The height of the truck is H_t = 13.5 feet. From the values obtained we see that:

a) The truck is not able to pass through the circular tunnel, because of H_c < H_t.

b) A priori it could be possible for the truck to pass through the tunnel with parabola's form, because of H_p > H_t, but we must check if the truck wide passes through the tunnel!

To analyze this situation, let's look in detail the graph of the parabola:

In the graph, we plotted the tunnel with parabola's form and the truck passing trough is centre, we have:

• in blue the parabola of height ,H_p = 16, and with axis of symmetry ,x = 18,,

,

• in red the height of the truck ,H_t = 13.5,,

,

• in black the sides of the truck, at distances ,x = 18 - 4 = 14, and ,x = 18 + 4 = 22,.

We see that the corners of the truck don't touch the parabola, so we conclude that the truck is able to pass through the tunnel with the parabola's form.