Given: Solution A is 35% salt and Solution B Is 65% salt
To Determine: How many ounces of each solutions A and B
Solution
Let the number of ounces for solution A be x, and the number of ounces for solution B be y
Since the total number of ounces is 120, then our first equation is

Since we have the percentage of salt in solution A and solution B, and the mixture, then the second equation would be
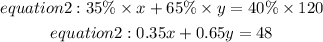
Let us compare the two equations together as shown below
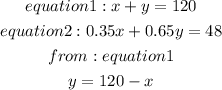
Substitute y intoequation 2

Let us substitute x into y
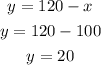
Hence, the ounces used for each solution would be
Solution A : 100 ounces
Solution B : 20 ounces