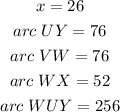First of all, let us find the value of x
Notice that the sum of central angles 4x and (2x+24) must be equal to 180° (half of the entire circle)
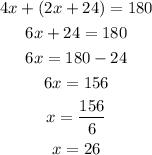
So, the value of x is 26
The arc UY is given by
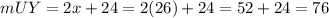
So, the arc UY is 76°
The arc VW must be equal to the arc UY since their central angles are vertically opposite angles.
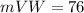
So, the arc VW is 76°
The arc WX must be half of the arc UV
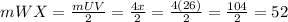
So, the arc WX is 52°
Finally, the arc WUY is given by
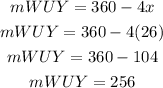
So, the arc WUY is 256°
Therefore, the arcs are