Question

Find each measure:z 4.rºUw(2x + 24)X=Arc UY =Ary WW=oArc WX =oArc WUY =Blank 1:Blank 2:Blank 3:Blank 4:Blank 5:

Answer 1

First of all, let us find the value of x

Notice that the sum of central angles 4x and (2x+24) must be equal to 180° (half of the entire circle)

`\begin{gathered} 4x+(2x+24)=180 \\ 6x+24=180 \\ 6x=180-24 \\ 6x=156 \\ x=(156)/(6) \\ x=26 \end{gathered}`

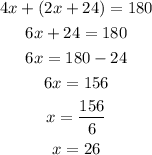
So, the value of x is 26

The arc UY is given by

`mUY=2x+24=2(26)+24\degree=52+24\degree=76\degree`

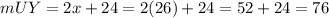
So, the arc UY is 76°

The arc VW must be equal to the arc UY since their central angles are vertically opposite angles.

`mVW=76\degree`

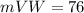
So, the arc VW is 76°

The arc WX must be half of the arc UV

`mWX=(mUV)/(2)=(4x)/(2)=(4(26))/(2)=(104)/(2)=52\degree`

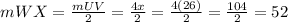
So, the arc WX is 52°

Finally, the arc WUY is given by

`\begin{gathered} mWUY=360\degree-4x \\ mWUY=360\degree-4(26)_{} \\ mWUY=360\degree-104\degree \\ mWUY=256\degree \end{gathered}`

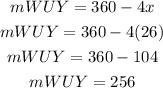
So, the arc WUY is 256°

Therefore, the arcs are

`\begin{gathered} x=26 \\ arc\; UY=76\degree \\ arc\; VW=76\degree \\ arc\; WX=52\degree \\ arc\; WUY=256\degree \end{gathered}`