The given expression is:
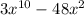
Part a: Factor the two terms as below:
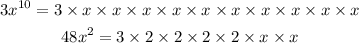
As seen above the common factor is 3 and x and x so it follows:

Take the GCF common from the expression to get:

Part b: The other bracket can be factored using the formula:

So it follows:
![\begin{gathered} 3x^2(x^8-16)=3x^2((x^4)^2-4^2)=3x^2(x^4-4)(x^4+4) \\ =3x^2(x^4+4)((x^2)^2-2^2) \\ =3x^2(x^4+4)(x^2-2)(x^2+2) \\ =3x^2(x^4+4)(x^2+2)(x-\sqrt[]{2})(x+\sqrt[]{2}) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/r2zepubtz5cmkld6mpw6rl5tvrc3mibtps.png)
In this way the expression is factored. The final value is the last line given above.