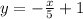For the given system:

If we divide the second equation by -1, we will obtain:

Which is the same as the first equation.
Since the system is compound of 2 equal equations, we conclude that the system has infinitely many solutions.
They must satisfy the following equation: