Quadratic Function
Given a quadratic function of the form:

The vertex of the parabola that represents the function is located at the x-coordinate:

If the value of a is positive, the function has a minimum value at the vertex and if a is negative, the function has a maximum value at the vertex.
We are given the amount of profit y, as a function of the selling price of each widget x:
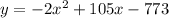
Here: a=-2, b=105, c=-773. Calculating the x-coordinate of the vertex:
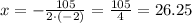
Now substitute in the function:

The maximum amount of profit the company can make is $605