Answer:
Explanation:
I'm assuming you provided the equation:
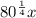
In general any nth root can be rewritten as:
![\sqrt[n]{x} = x^{(1)/(n)}](https://img.qammunity.org/2023/formulas/mathematics/high-school/159al6jcro6y27zsozvw0jjmyap6b2aez6.png)
We can refer to the law of exponents, to prove why this is the case.
You may recall from the law of exponents, the power of a power rule:
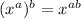
So if we take the value:
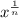 and raise it to the nth power as such:
and raise it to the nth power as such:
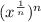 , we can multiply the exponents to get:
, we can multiply the exponents to get:
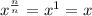
This is by definition the nth root, if we can raise this to the nth power to get the original value.
So we can rewrite raising x to the one-fourth, as the fourth root of 80.
From here we get:
![x\sqrt[4]{80}](https://img.qammunity.org/2023/formulas/mathematics/high-school/j24eymvbrtdpe6oe6xgc1ym861356nj79e.png)
Assuming your equation was actually:
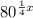
We can actually use our power to a power rule, since it goes both ways.
We can rewrite:
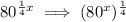
From here we can use our nth root definition which we proved above to get the following:
![\sqrt[4]{80^x}](https://img.qammunity.org/2023/formulas/mathematics/high-school/srz0hlmfct3rmonef8ff1ndlhql62wzk6v.png)
Note: We could've rewritten the expression as such
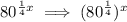 , since multiply the exponents would give us our original expression, with further simplification giving us:
, since multiply the exponents would give us our original expression, with further simplification giving us:
![(\sqrt[4]{80})^x](https://img.qammunity.org/2023/formulas/mathematics/high-school/5bbkobtto02vf74rhi7eifovdvra8ejszo.png) , and this would give us the same expression, both are equally valid (except in certain cases where the domain may change as a result)
, and this would give us the same expression, both are equally valid (except in certain cases where the domain may change as a result)