Given the function:
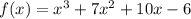
Let's list the steps to find the zeros of the function.
To find the zeros of the function, apply the following steps:
• Step 1:
Set the function, f(x) = 0:
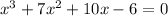
• Step 2:
Factor the expression on the left using the rational roots test

• Step 3:
Divide the polynomial (x³+7x²+10x-6) by (x+3).
After the division, we have:
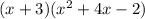
• Step 4:
Write the given polynomial as a set of factors
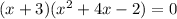
Step 5:
Set each individual factor to zero
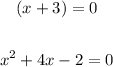
Step 6:
Solve for x in the first factor: (x + 3) = 0
Step 7:
Solve for x in the second factor: (x² + 4x - 2) = 0
• ANSWER:
• Step 1: Set the function f(x) = 0
,
• Step 2: Factor the expression on the left using the rational roots test
,
• Step 3: Divide the polynomial by the factor derived in step 2.
,
• Step 4: Write the factor gotten in step 2 and the quotient in step 3 as a set of factors.
,
• Step 5: Set each individual factor to zero.
,
• Step 6: Solve for x in the first factor
,
• Step 7: Solve for x in the second factor.