We have that the equation to find the area of a circle sector is the following:
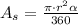
where r is the radius and and alpha is the angle in degrees.
In this case, since the diameter is 20 cm, then the radius is half of 20 (r = 10), also, the area of the sector is 15pi square centimeters. Using the formula, we get:
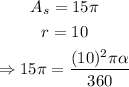
solving for alpha, we get the following:
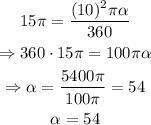
therefore, the measure of the arc is 54 degrees