Question

The diameter of a circle is 20 centimeters. What is the angle measure of an arc bounding a sector with area 15pi square centimeters?

Answer 1

We have that the equation to find the area of a circle sector is the following:

`A_s=(\pi\cdot r^2\alpha)/(360)`

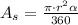
where r is the radius and and alpha is the angle in degrees.

In this case, since the diameter is 20 cm, then the radius is half of 20 (r = 10), also, the area of the sector is 15pi square centimeters. Using the formula, we get:

`\begin{gathered} A_s=15\pi \\ r=10 \\ \Rightarrow15\pi=((10)^2\pi\alpha)/(360) \end{gathered}`

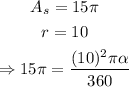
solving for alpha, we get the following:

`\begin{gathered} 15\pi=((10)^2\pi\alpha)/(360) \\ \Rightarrow360\cdot15\pi=100\pi\alpha \\ \Rightarrow\alpha=(5400\pi)/(100\pi)=54 \\ \alpha=54\degree \end{gathered}`

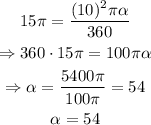
therefore, the measure of the arc is 54 degrees