Question

Please help me solve this. what is the probability of tossing heads on a coin twice and rolling a number greater than four on a number cube?

Answer 1

You have to calculate the probability of tossing heads twice and a number greater than four on a dice.

Let "H" represent the event "toss a coin and the observation is head"

When you toss a con there are two possible outcomes "heads" (H) and "tail" (T), if the coin is balanced, then both outcomes have the same probability of occurring, which is equal to 1/2, so

`P(H)=P(T)=(1)/(2)`

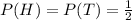
Let "A" represent the event "roll a dice and the number is greater than four"

A dice has 6 faces numbered from 1 to 6, there are two values greater than 4, which are "5" and "6".

So, for event A, there are 2 successful outcomes out of 6 possible outcomes, the probability of the event is equal to the quotient between the number of successes and the total outcomes:

`\begin{gathered} P(A)=(2)/(6) \\ P(A)=(1)/(3) \end{gathered}`

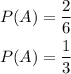
Now that you know the probabilities for the events, you can calculate the asked probability which is:

Probability of tossing a head and tossing a head and rolling a number greater than 4.

You can symbolize this probability as the intersection between the events:

`P(H\cap H\cap A)`

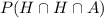
These events are independent, so the probability of the intersection is equal to the product of each individual probability:

`\begin{gathered} P(H\cap H\cap A)=P(H)\cdot P(H)\cdot P(A) \\ (1)/(2)\cdot(1)/(2)\cdot(1)/(3)=(1)/(4)\cdot(1)/(3)=(1)/(12) \end{gathered}`

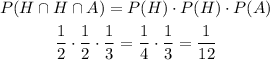
The probability is 1/12 or 8.33%