You have to calculate the probability of tossing heads twice and a number greater than four on a dice.
Let "H" represent the event "toss a coin and the observation is head"
When you toss a con there are two possible outcomes "heads" (H) and "tail" (T), if the coin is balanced, then both outcomes have the same probability of occurring, which is equal to 1/2, so
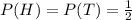
Let "A" represent the event "roll a dice and the number is greater than four"
A dice has 6 faces numbered from 1 to 6, there are two values greater than 4, which are "5" and "6".
So, for event A, there are 2 successful outcomes out of 6 possible outcomes, the probability of the event is equal to the quotient between the number of successes and the total outcomes:
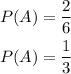
Now that you know the probabilities for the events, you can calculate the asked probability which is:
Probability of tossing a head and tossing a head and rolling a number greater than 4.
You can symbolize this probability as the intersection between the events:
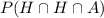
These events are independent, so the probability of the intersection is equal to the product of each individual probability:
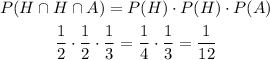
The probability is 1/12 or 8.33%