From the statement of the problem, we know that:
• the height of the tree is 80ft,
,
• the first angle of inclination is 68°,
,
• the second angle of inclination is 41°.
We define:
• d as the distance for the first angle of inclination,
,
• x as the distance that Corey walk to the position for the second angle of inclination.
Using the data of the problem, we make the following graph:
From the triangle, we see two triangles:
1) △BTA1, with:
• θ = angle = ,68°,.
,
• OS = opposite side to the angle = 80ft,
,
• AS = adjacent side to the angle = ,d,,
2) △BTA2, with:
• θ = angle = ,41°,.
,
• OS = opposite side to the angle = 80ft,
,
• AS = adjacent side to the angle =, x + d,,
Now from trigonometry, we have the following relation:
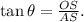
Using this equation for each triangle, we get the following equations:
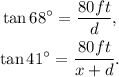
From the first equation, we get the value of d:

Solving the second equation for x and replacing the value of d, we get:
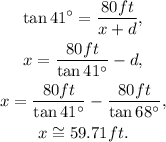
Answer
Corey stepped back 59.71ft to gain a better view of the bird.