11) We have the vertices F(-2,2), G(-2,-4) and H(-4,-4).
We have to apply a dilation with center at (0,0) and a factor of dilation of k = 3.
A dilation with center at (0,0) has the following rule:
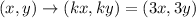
Then, we can apply this rule to the three vertices as:
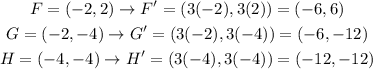
We can then graph the pre-image and the image as: