We have points (-2,5), (-1,2) and (0,1) and we need to find the quadratic equation that pass through these 3 points.
We have 3 parameters to find, but, if we look at the points the point (0,1) is already telling us the y-intercept (the value of y when x=0).
Then, c=1.
We can then start with the function as:
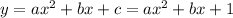
Replacing the values of (x,y) for the remaining 2 points we will get a system of equations with two equations and two unknowns:
For point (-2,5)
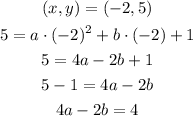
For point (-1,2)
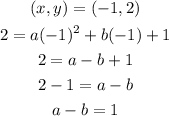
Then, we have the equations:
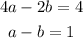
We can solve it by elimination as:
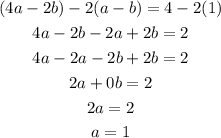
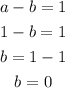
With a=1 and b=0, the equation becomes:
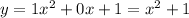
Answer: y=x^2+1
NOTE: 3 points to determine the quadratic equation.
We have points (x1,y1), (x2,y2) and (x3,y3).
Then we can write for each one:
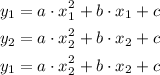
That would give us a 3 equations - 3 unknown system, being a, b and c the unknowns we have to solve:
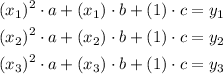
For example, with points (-2,5), (-1,2) and (0,1) we would get:
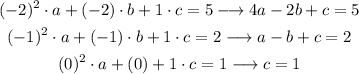
The last equation gives us the c coefficient directly (c=1), and then we can solve it from there as we did.