step 1
Find out the value of
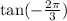
Remember that
2pi/3=2(180)/3=120 degrees
the angle belonging to the third quadrant
the tangent in III quadrant is positive
so
tan(-2pi/3)=tan(180-120)=tan(60)
and
![\begin{gathered} \tan (60^o)=\sqrt[]{3} \\ \tan (-(2\pi)/(3))=\sqrt[]{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/8xjj7cvnsoem5ffj6a84s8njxh69sn7kdx.png)
step 2
Find out the value of
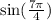
we have that
7pi/4=7*180/4=315 degrees
the angle lies on the IV quadrant
the sine is negative
sin(7pi/4)=sin (315)=-sin (360-315)=-sin(45)
![\begin{gathered} \sin (45^o)=\frac{\sqrt[]{2}}{2} \\ \sin \text{ (}(7\pi)/(4))=-\frac{\sqrt[]{2}}{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/t778entc5s8q89jbrup5xpmrqan04041nr.png)
step 3
Find out the value of
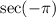
sec(-pi)=sec(pi)=1/cos(pi)=1/-1=-1
step 4
substitute the given values in the original expression
![\frac{\sqrt[]{3}}{\frac{-\sqrt[]{2}}{2}}-(-1)](https://img.qammunity.org/2023/formulas/mathematics/college/9rzqej1qrxuhaiv332jzz70r9k9p754ri6.png)
![-\frac{2\sqrt[]{3}}{\sqrt[]{2}}+1=\frac{-2\sqrt[]{3}+\sqrt[]{2}}{\sqrt[]{2}}](https://img.qammunity.org/2023/formulas/mathematics/college/xjmeg2m9rce1kmjkqugr8jd7p8js9zqst4.png)
simplify
![\frac{-2\sqrt[]{3}+\sqrt[]{2}}{\sqrt[]{2}}\cdot\frac{\sqrt[]{2}}{\sqrt[]{2}}=\frac{-2\sqrt[]{6}+2}{2}=-\sqrt[]{6}+1](https://img.qammunity.org/2023/formulas/mathematics/college/hhu0czuejah4yskaeorwkyk782613l7x5w.png)