Question

During summer vacation, you charge $12 per hour for golf lessons and a registration fee of $50. If you make$98 one day, how many hours did you spend teaching lessons? Let g represent golf lessons, write an equationfor the situation.

Answer 1

The question indicates a linear equation showing the relationship between the fee charged on golf lessons and the hour spent.

The linear equation can be represented by;

`\begin{gathered} y=r+g \\ \text{where y is the total f}ee\text{ charged} \\ r\text{ is the registration fe}e \\ g\text{ is the golf lesson fe}e \end{gathered}`

Given:

`\begin{gathered} r=\text{ \$50} \\ g=12t,\text{ where t is the number of hours for the golf lesson} \\ y=\text{ \$98} \end{gathered}`

From the above,

The equation can be re-written as;

`y=50+12t`

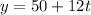
Hence, substituting the total amount made for the day into the equation to get the number of hours used teaching the lessons;

`\begin{gathered} 98=50+12t \\ \text{Collecting the like terms to get t,} \\ 98-50=12t \\ 48=12t \\ \text{Dividing both sides by 12;} \\ t=(48)/(12) \\ t=4\text{hours} \end{gathered}`

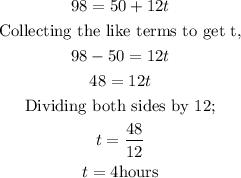
Therefore, 4 hours was spent teaching the lessons for the day $98 was made.