Solution:
The question indicates a linear equation showing the relationship between the fee charged on golf lessons and the hour spent.
The linear equation can be represented by;
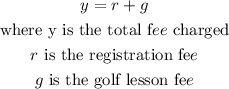
Given:
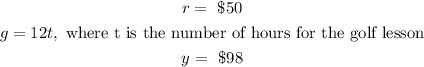
From the above,
The equation can be re-written as;
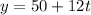
Hence, substituting the total amount made for the day into the equation to get the number of hours used teaching the lessons;
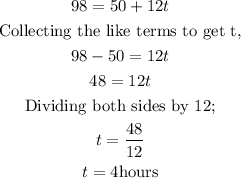
Therefore, 4 hours was spent teaching the lessons for the day $98 was made.